A proof game is a type of retrograde analysis chess problem - the solver must construct a game starting from the initial chess position, which ends with a given position (thus proving that the position is reachable) after a specified number of moves. A proof game is called a shortest proof game if no shorter solution exists. In this case the task is simply to construct the shortest possible game ending with the given position.
A shortest proof game that has only 2 pieces left (the kings, obviously) is called a "massacre" shortest proof game. The search for such proof games started in 1895, when Sam Loyd published one in the New York Clipper - unfortunately with many solutions in 17 moves, which does not satisfy the requirement of having a unique solution.
Sam Loyd
New York Clipper 1895
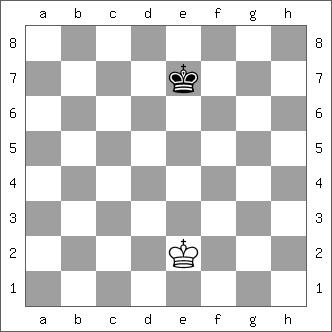
PG 17 (non-unique) (1+1)
In 1994, two German chess problem composers, Gerd Wilts and Norbert Geisler, started a computer-assisted search for a 2-King proof game in 17 moves. Their search only uncovered a conditional problem (to have a unique solution the Black's second move must be a capture):
Gerd Wilts, Norbert Geisler
Special Prize, Die Schwalbe 1994
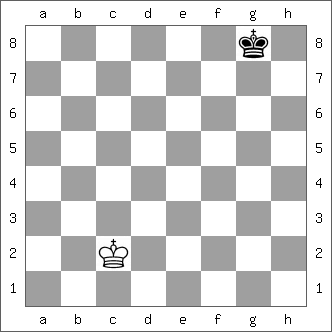
PG 17 (1+1)
Black's second move is a capture
In 2004 Gerd Wilts found a fairy-chess 2-King proof game (by using the Einstein Chess fairy condition), and subsequently many other examples with fairy conditions were published (by the Dutch Joost de Heer in 2009).
Finally, the first realization of this task in orthodox chess without additional conditions is the result of extensive computer searches performed between 2004 and 2012 by the Canadian François Labelle! This composition was published in the April - June 2012 issue of the US chess problem magazine StrateGems, together with a very interesting article describing the methods and pruning strategies used for the search, as well as a few proof games with 3 pieces (349 such proof games had been obtained as a by-product of the search).
Here is the first absolute massacre proof game without conditions, for your solving enjoyment!
François Labelle, Canada
P0330 StrateGems 58, April - June 2012

PG 19.5 (1+1)
A shortest proof game that has only 2 pieces left (the kings, obviously) is called a "massacre" shortest proof game. The search for such proof games started in 1895, when Sam Loyd published one in the New York Clipper - unfortunately with many solutions in 17 moves, which does not satisfy the requirement of having a unique solution.
Sam Loyd
New York Clipper 1895
PG 17 (non-unique) (1+1)
In 1994, two German chess problem composers, Gerd Wilts and Norbert Geisler, started a computer-assisted search for a 2-King proof game in 17 moves. Their search only uncovered a conditional problem (to have a unique solution the Black's second move must be a capture):
Gerd Wilts, Norbert Geisler
Special Prize, Die Schwalbe 1994
PG 17 (1+1)
Black's second move is a capture
In 2004 Gerd Wilts found a fairy-chess 2-King proof game (by using the Einstein Chess fairy condition), and subsequently many other examples with fairy conditions were published (by the Dutch Joost de Heer in 2009).
Finally, the first realization of this task in orthodox chess without additional conditions is the result of extensive computer searches performed between 2004 and 2012 by the Canadian François Labelle! This composition was published in the April - June 2012 issue of the US chess problem magazine StrateGems, together with a very interesting article describing the methods and pruning strategies used for the search, as well as a few proof games with 3 pieces (349 such proof games had been obtained as a by-product of the search).
Here is the first absolute massacre proof game without conditions, for your solving enjoyment!
François Labelle, Canada
P0330 StrateGems 58, April - June 2012
PG 19.5 (1+1)


Comment